Hands-on_Ex04

Author

Linsen Lu

Getting Start

Installing and loading the packages

pacman::p_load(ggdist, ggridges, ggthemes,
               colorspace, tidyverse, ggstatsplot, 
               tidyverse, plotly, crosstalk, DT, 
               ggdist, gganimate, FunnelPlotR, knitr)

Importing data

exam <- read_csv("data04/Exam_data_03.csv")

covid19 <- read_csv("data04/COVID-19_DKI_Jakarta.csv") %>%
  mutate_if(is.character, as.factor)

Visualising Distribution

Visualising Distribution with Ridgeline Plot

Plotting ridgeline graph: ggridges method

ggplot(exam, 
       aes(x = ENGLISH, 
           y = CLASS)) +
  geom_density_ridges(
    scale = 3,
    rel_min_height = 0.01,
    bandwidth = 3.4,
    fill = lighten("#7097BB", .3),
    color = "white"
  ) +
  scale_x_continuous(
    name = "English grades",
    expand = c(0, 0)
    ) +
  scale_y_discrete(name = NULL, expand = expansion(add = c(0.2, 2.6))) +
  theme_ridges()

Varying fill colors along the x axis

ggplot(exam, 
       aes(x = ENGLISH, 
           y = CLASS,
           fill = stat(x))) +
  geom_density_ridges_gradient(
    scale = 3,
    rel_min_height = 0.01) +
  scale_fill_viridis_c(name = "Temp. [F]",
                       option = "C") +
  scale_x_continuous(
    name = "English grades",
    expand = c(0, 0)
  ) +
  scale_y_discrete(name = NULL, expand = expansion(add = c(0.2, 2.6))) +
  theme_ridges()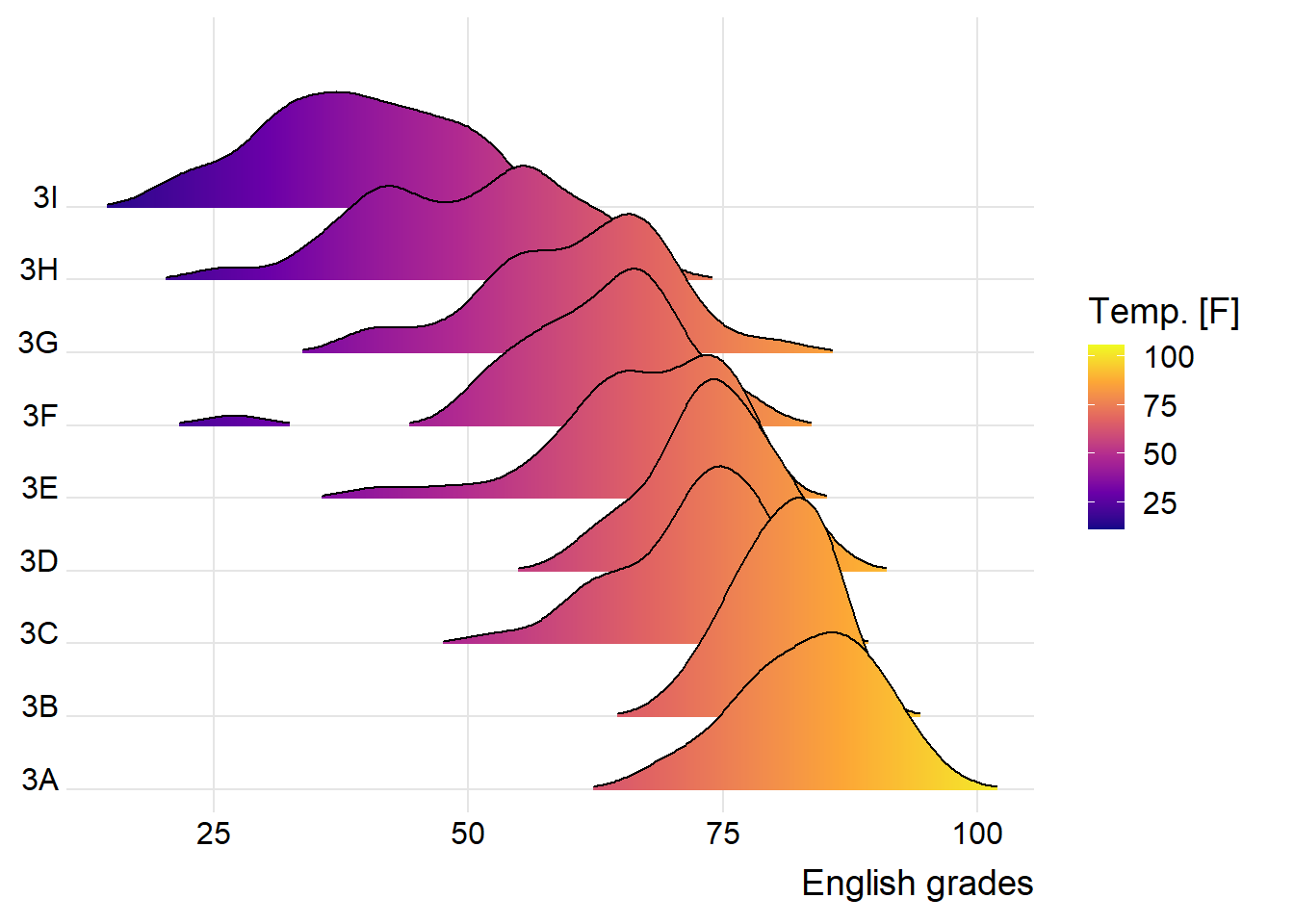

Mapping the probabilities directly onto colour

ggplot(exam,
       aes(x = ENGLISH, 
           y = CLASS, 
           fill = 0.5 - abs(0.5-stat(ecdf)))) +
  stat_density_ridges(geom = "density_ridges_gradient", 
                      calc_ecdf = TRUE) +
  scale_fill_viridis_c(name = "Tail probability",
                       direction = -1) +
  theme_ridges()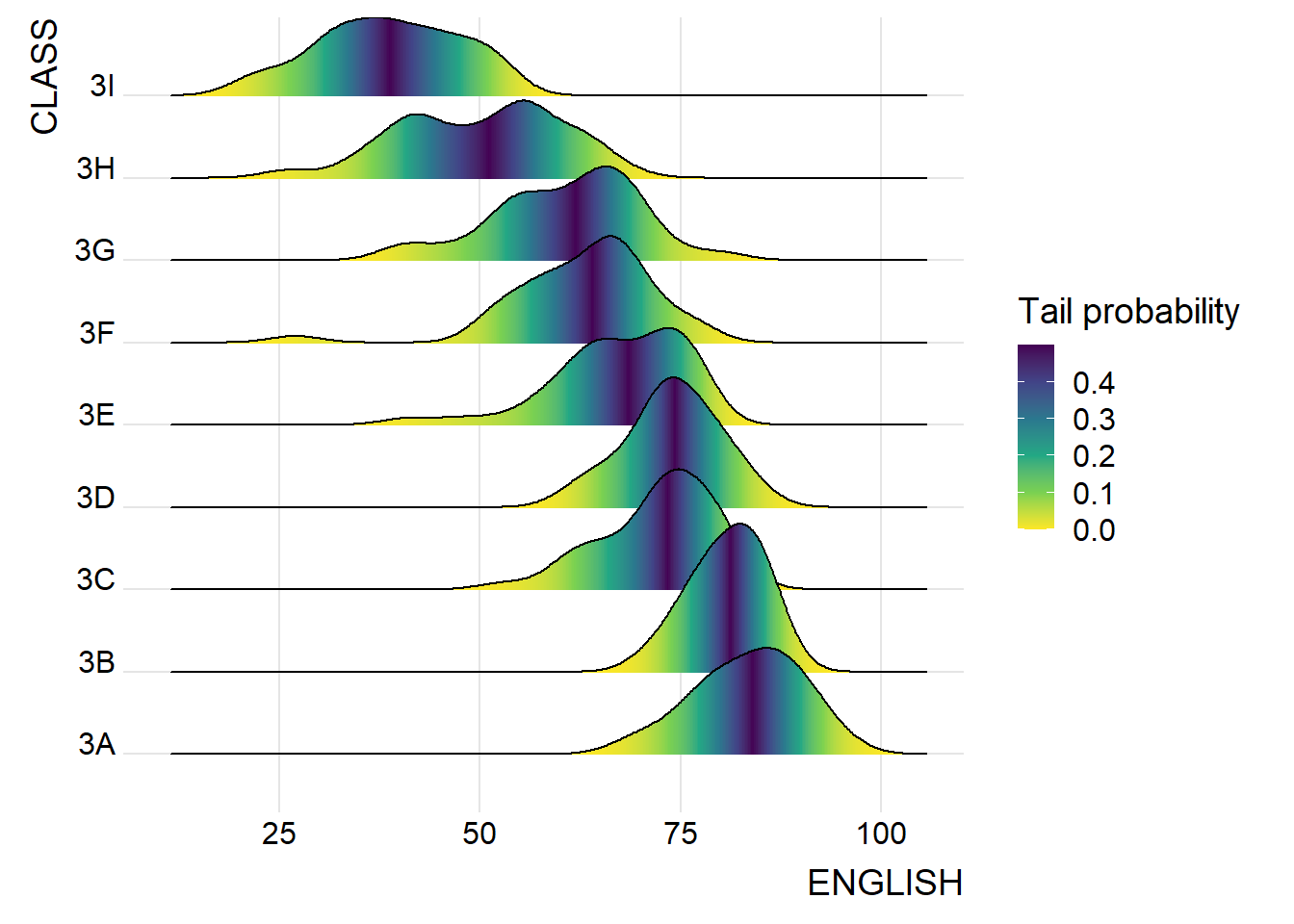

Ridgeline plots with quantile lines

ggplot(exam,
       aes(x = ENGLISH, 
           y = CLASS, 
           fill = factor(stat(quantile))
           )) +
  stat_density_ridges(
    geom = "density_ridges_gradient",
    calc_ecdf = TRUE, 
    quantiles = 4,
    quantile_lines = TRUE) +
  scale_fill_viridis_d(name = "Quartiles") +
  theme_ridges()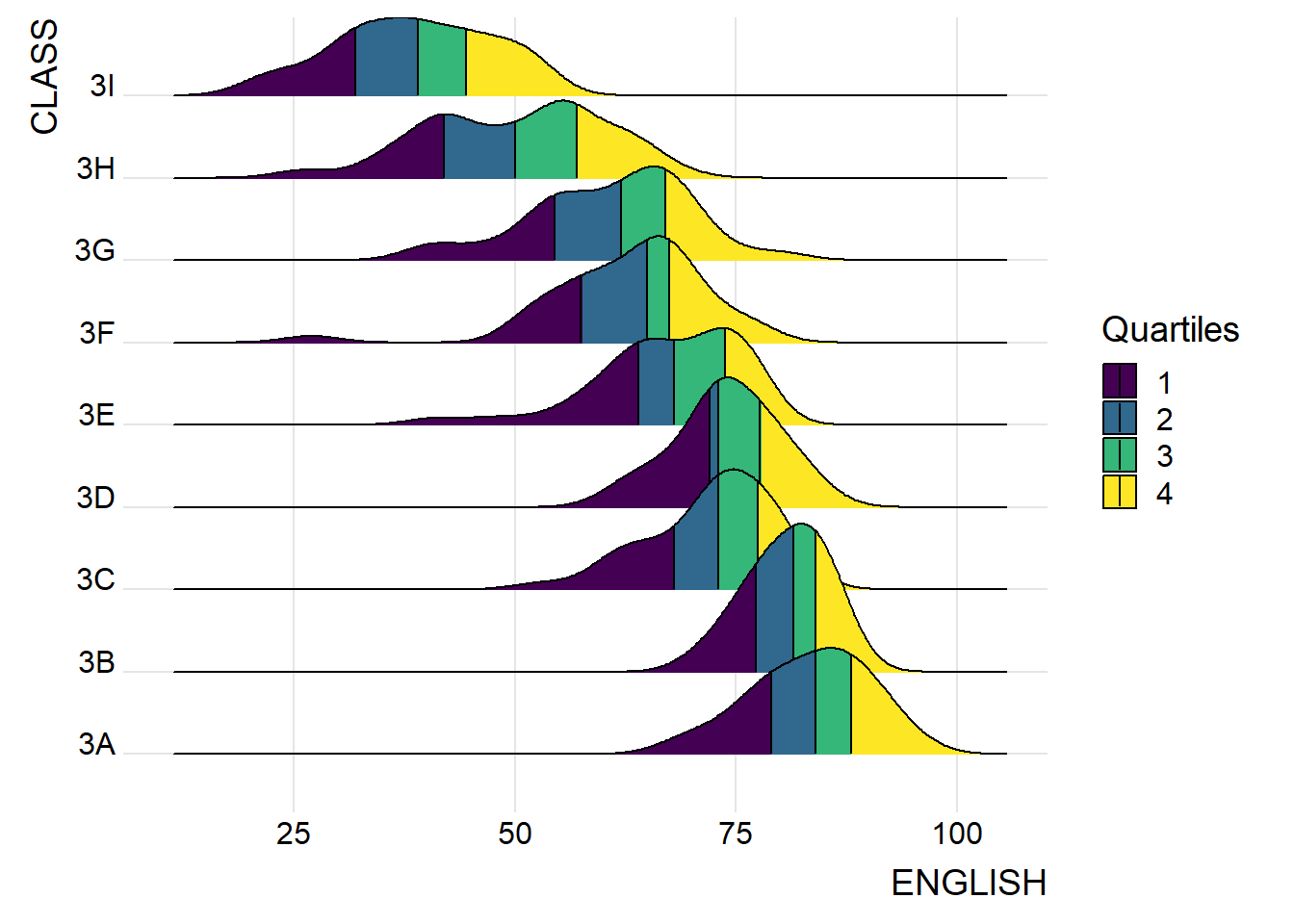

ggplot(exam,
       aes(x = ENGLISH, 
           y = CLASS, 
           fill = factor(stat(quantile))
           )) +
  stat_density_ridges(
    geom = "density_ridges_gradient",
    calc_ecdf = TRUE, 
    quantiles = c(0.025, 0.975)
    ) +
  scale_fill_manual(
    name = "Probability",
    values = c("#FF0000A0", "#A0A0A0A0", "#0000FFA0"),
    labels = c("(0, 0.025]", "(0.025, 0.975]", "(0.975, 1]")
  ) +
  theme_ridges()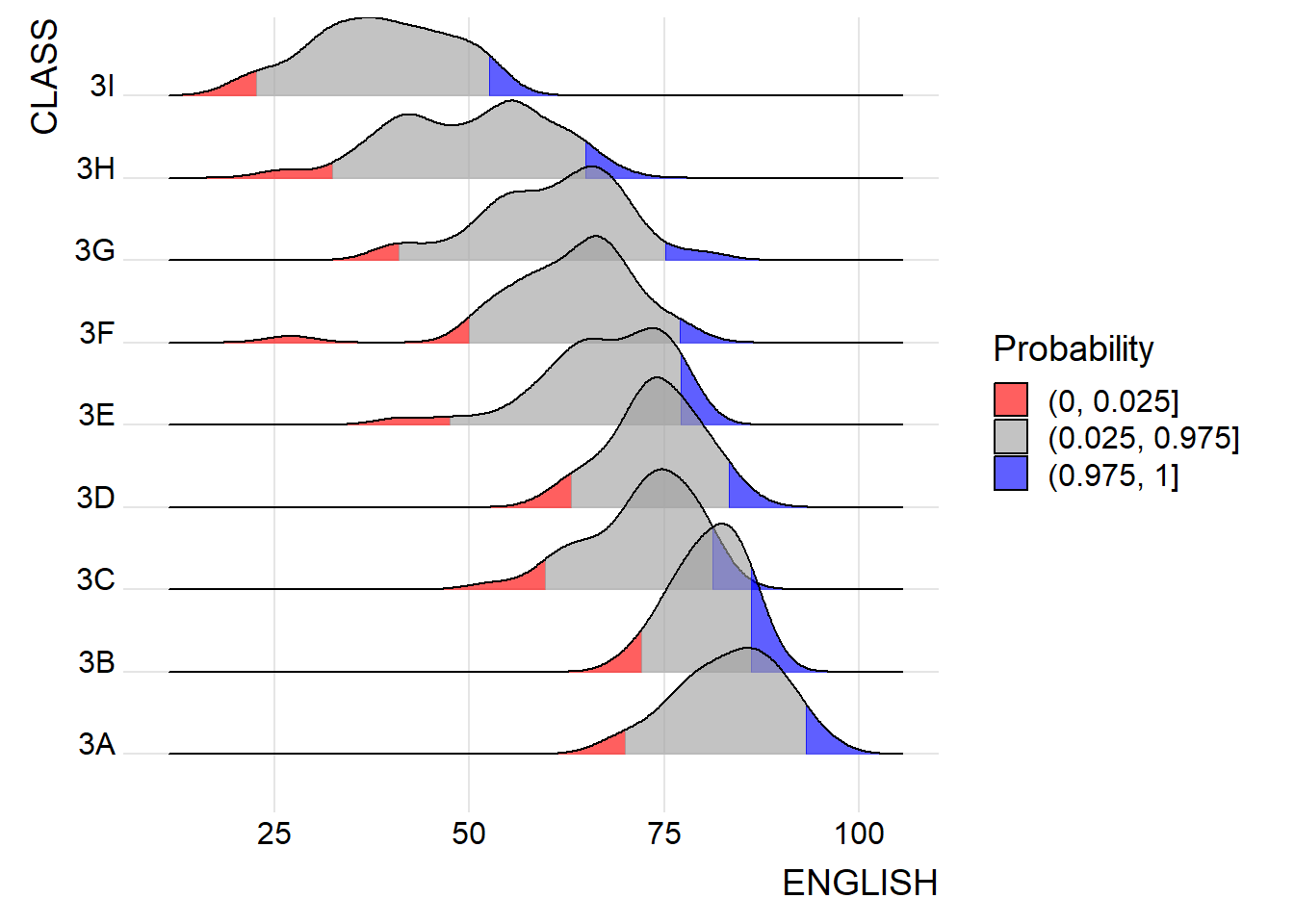

Visualising Distribution with Raincloud Plot

Plotting a Half Eye graph

ggplot(exam, 
       aes(x = RACE, 
           y = ENGLISH)) +
  stat_halfeye(adjust = 0.5,
               justification = -0.2,
               .width = 0,
               point_colour = NA)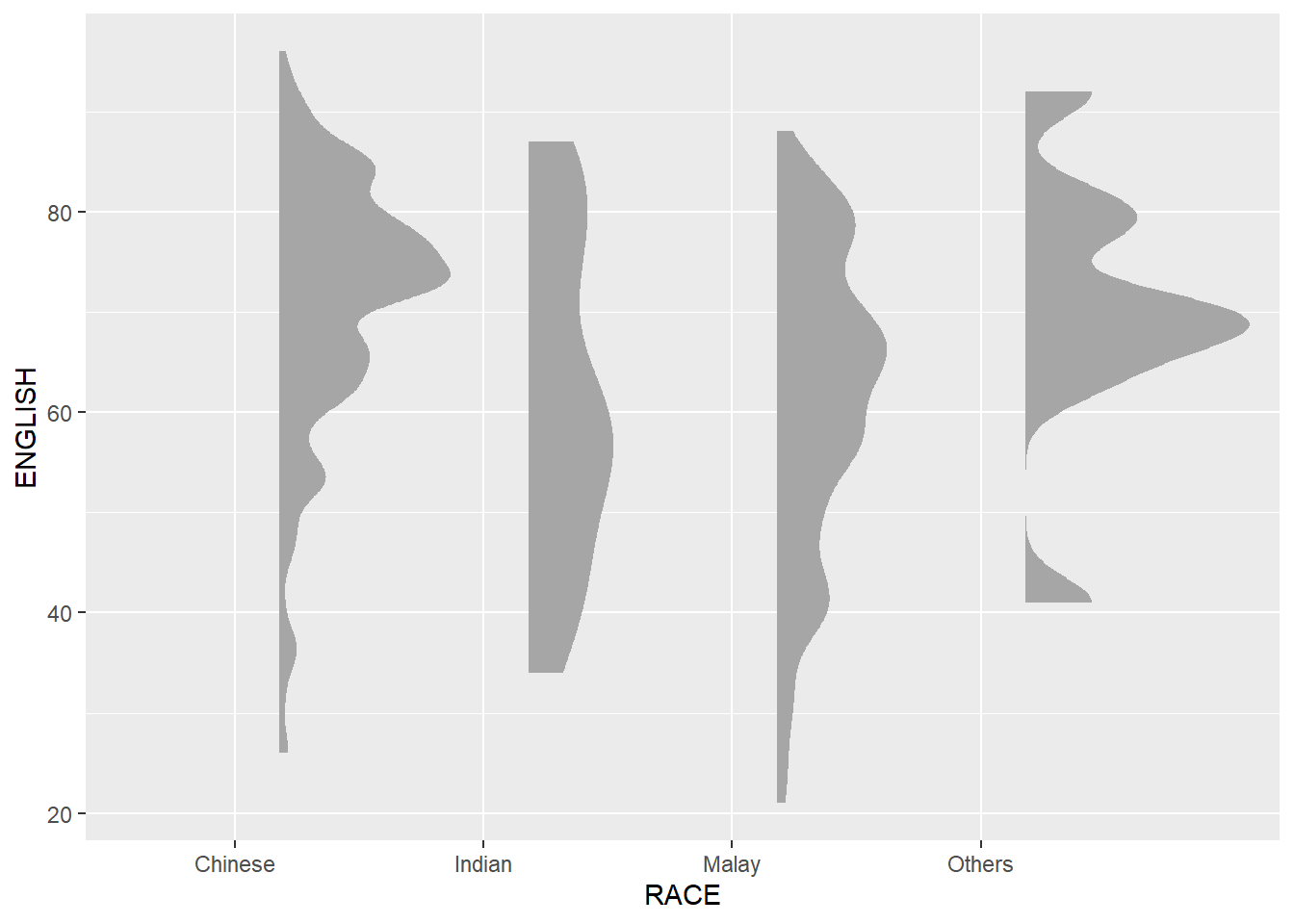

Adding the boxplot with geom_boxplot()

ggplot(exam, 
       aes(x = RACE, 
           y = ENGLISH)) +
  stat_halfeye(adjust = 0.5,
               justification = -0.2,
               .width = 0,
               point_colour = NA) +
  geom_boxplot(width = .20,
               outlier.shape = NA)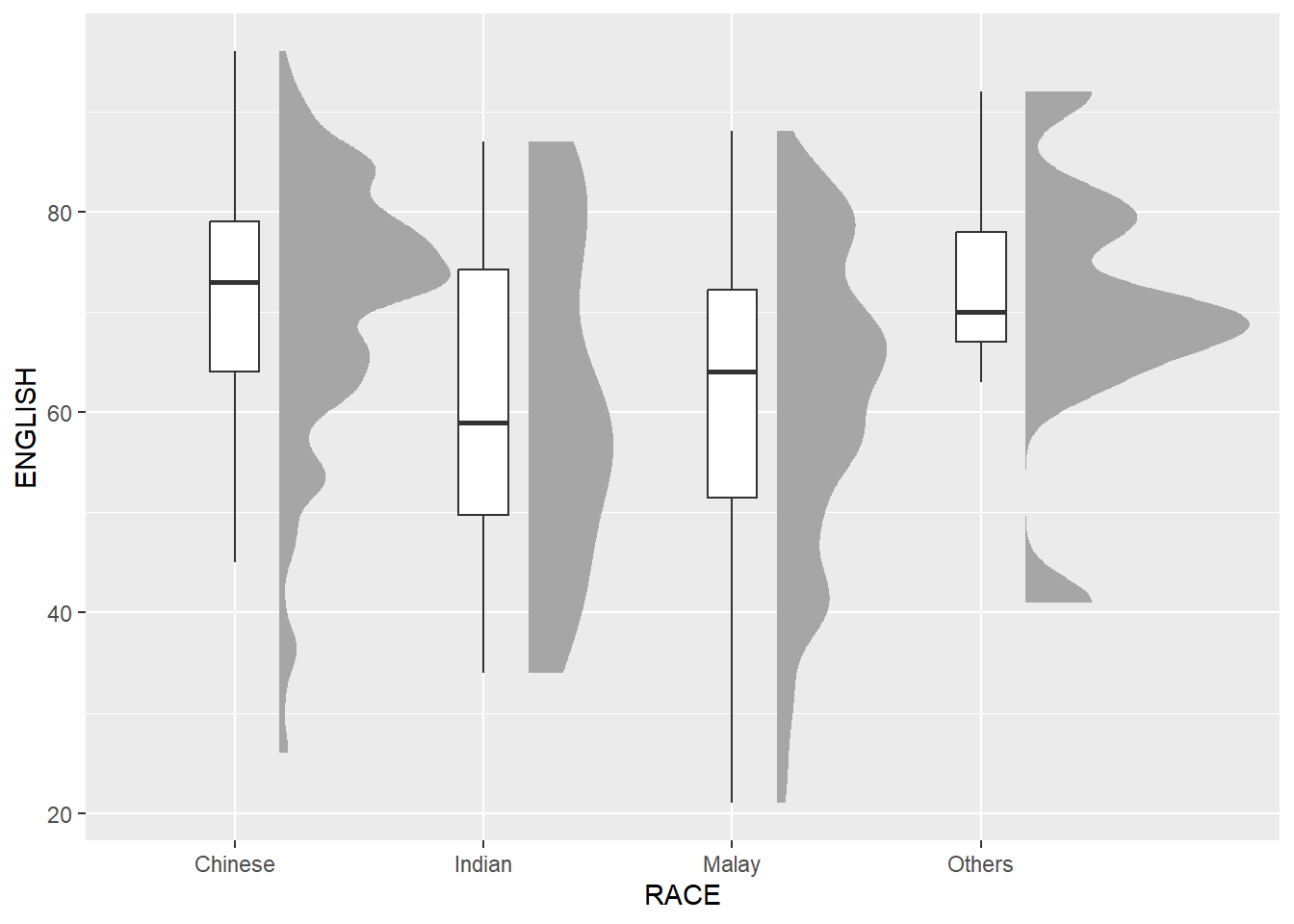

Adding the Dot Plots with stat_dots()

ggplot(exam, 
       aes(x = RACE, 
           y = ENGLISH)) +
  stat_halfeye(adjust = 0.5,
               justification = -0.2,
               .width = 0,
               point_colour = NA) +
  geom_boxplot(width = .20,
               outlier.shape = NA) +
  stat_dots(side = "left", 
            justification = 1.2, 
            binwidth = .5,
            dotsize = 2)

Finishing touch

ggplot(exam, 
       aes(x = RACE, 
           y = ENGLISH)) +
  stat_halfeye(adjust = 0.5,
               justification = -0.2,
               .width = 0,
               point_colour = NA) +
  geom_boxplot(width = .20,
               outlier.shape = NA) +
  stat_dots(side = "left", 
            justification = 1.2, 
            binwidth = .5,
            dotsize = 1.5) +
  coord_flip() +
  theme_economist()

Visual Statistical Analysis

Statistical Tests

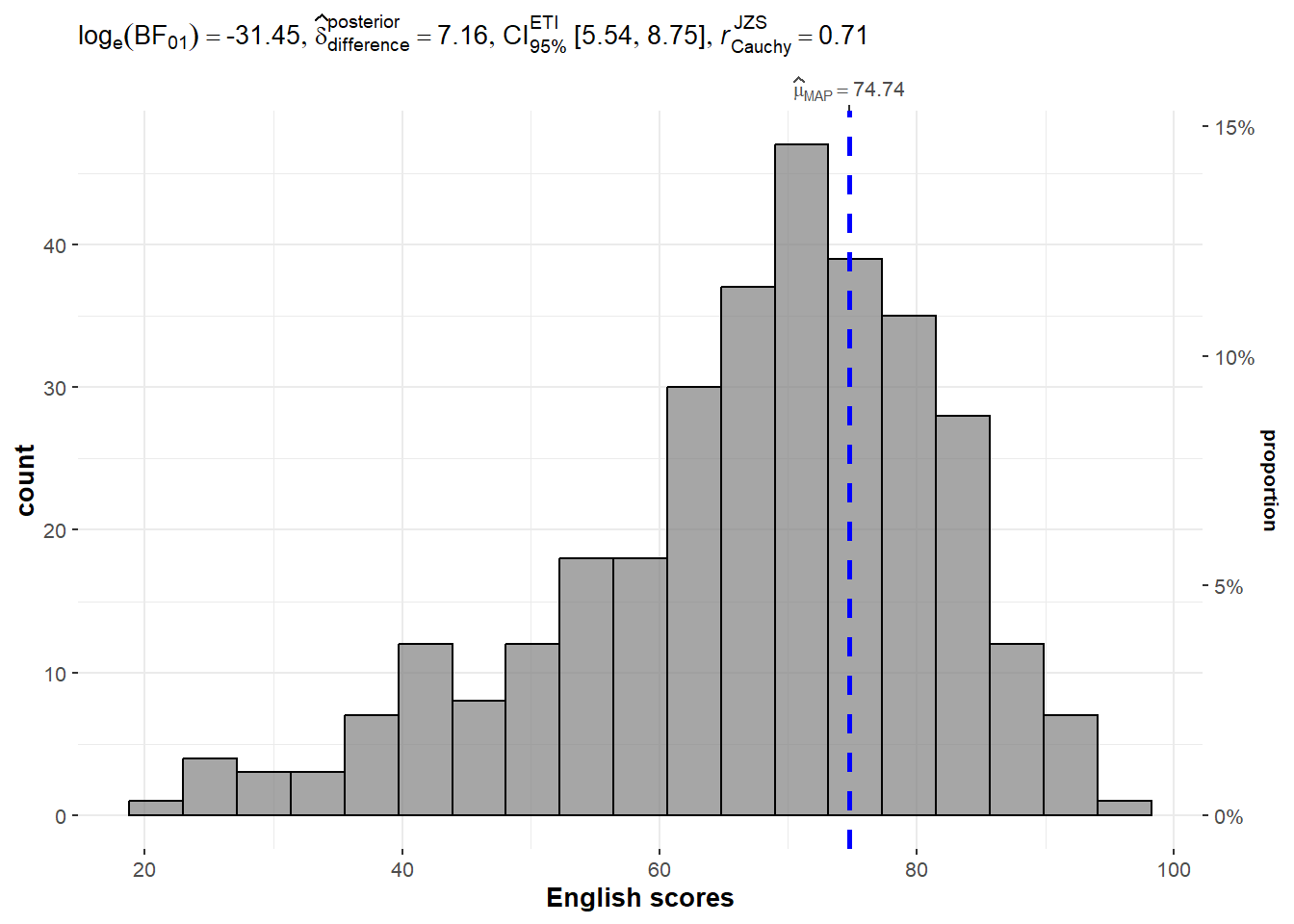
**One-sample test: gghistostats() method**

set.seed(1234)

gghistostats(
  data = exam,
  x = ENGLISH,
  type = "bayes",
  test.value = 60,
  xlab = "English scores"
)

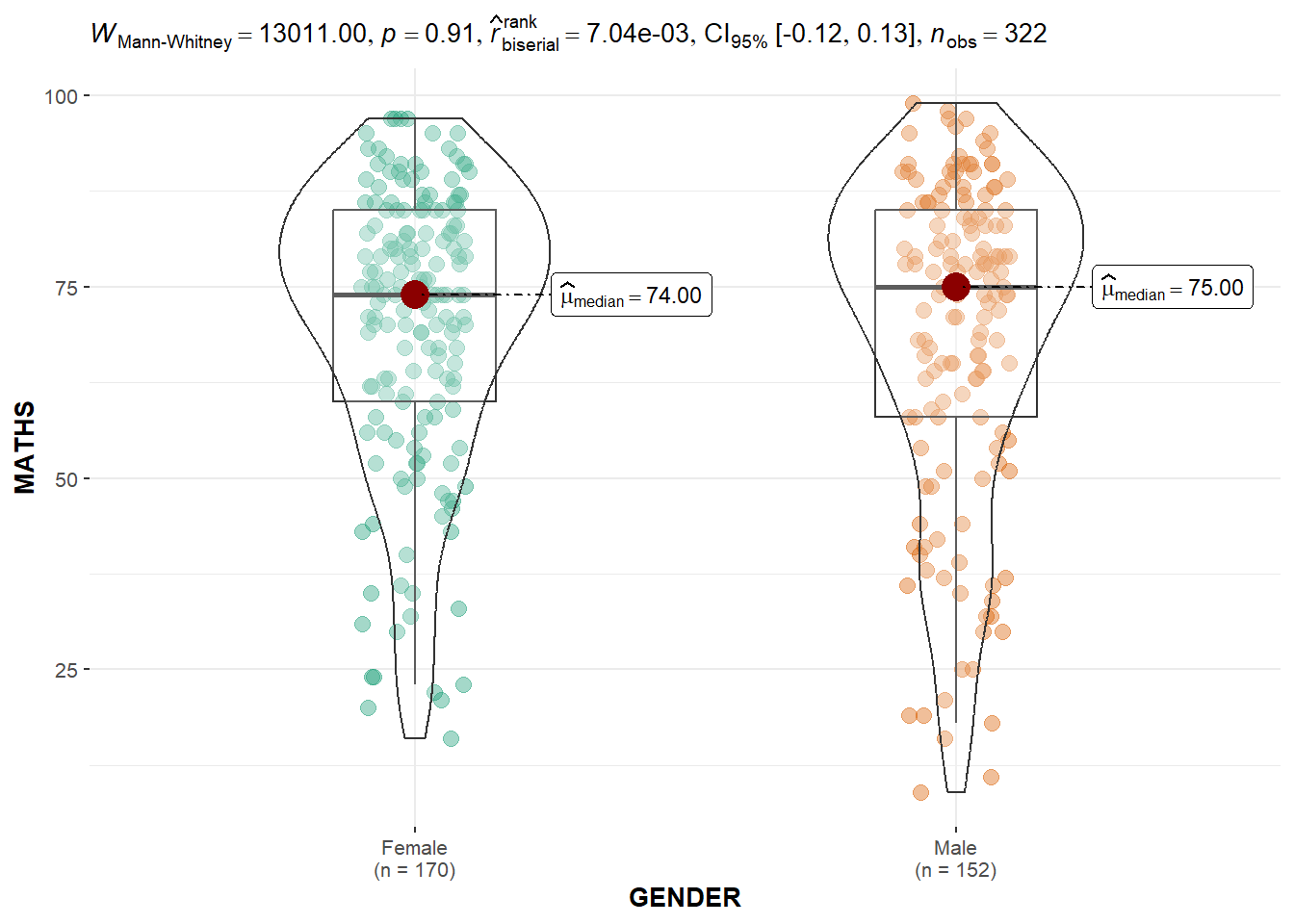
Two-sample mean test: ggbetweenstats()

ggbetweenstats(
  data = exam,
  x = GENDER, 
  y = MATHS,
  type = "np",
  messages = FALSE
)

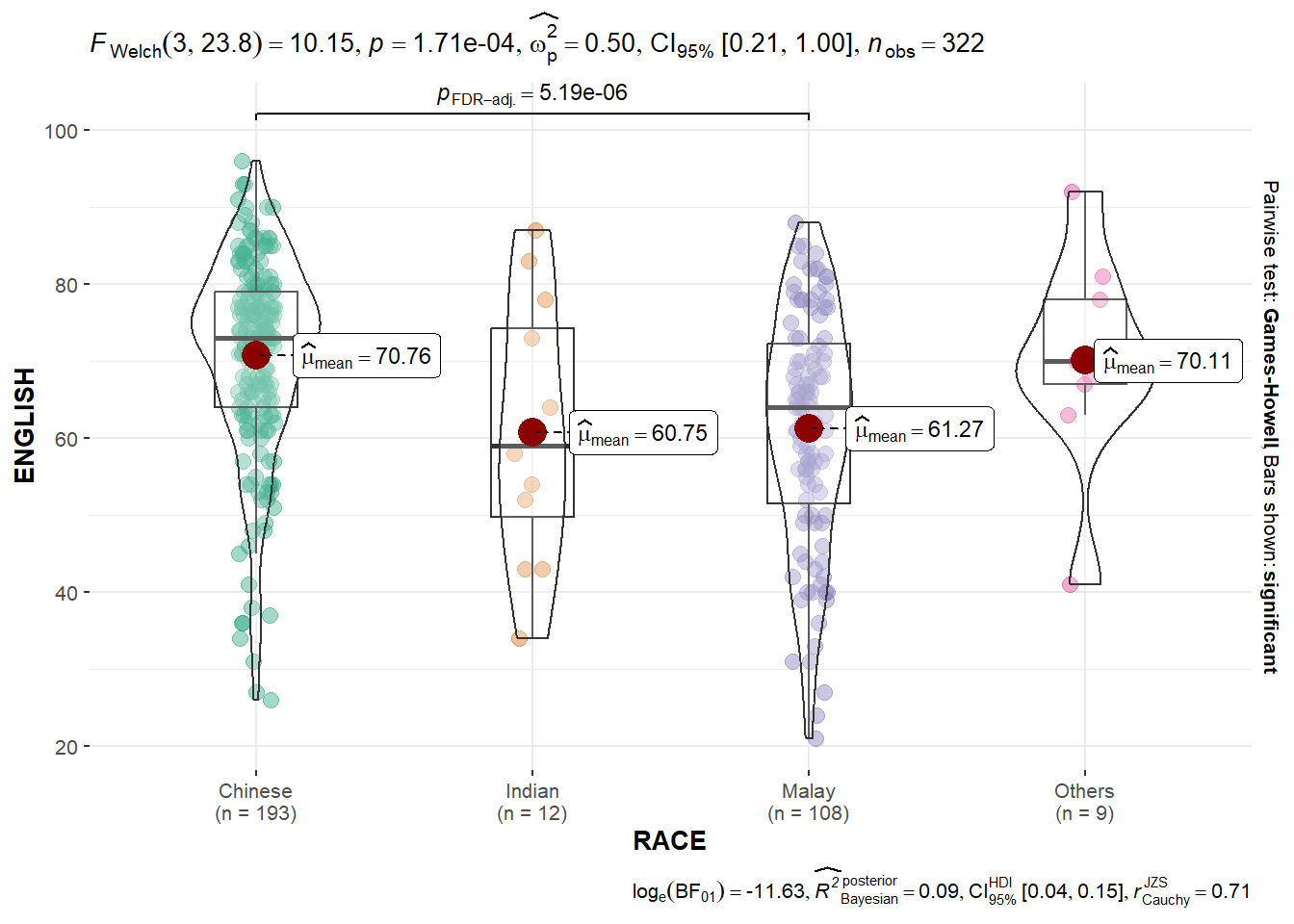
**Oneway ANOVA Test: ggbetweenstats() method**

ggbetweenstats(
  data = exam,
  x = RACE, 
  y = ENGLISH,
  type = "p",
  mean.ci = TRUE, 
  pairwise.comparisons = TRUE, 
  pairwise.display = "s",
  p.adjust.method = "fdr",
  messages = FALSE
)

**Significant Test of Association (Depedence) : ggbarstats() methods**

exam1 <- exam %>% 
  mutate(MATHS_bins = 
           cut(MATHS, 
               breaks = c(0,60,75,85,100))
)

ggbarstats(exam1, 
           x = MATHS_bins, 
           y = GENDER)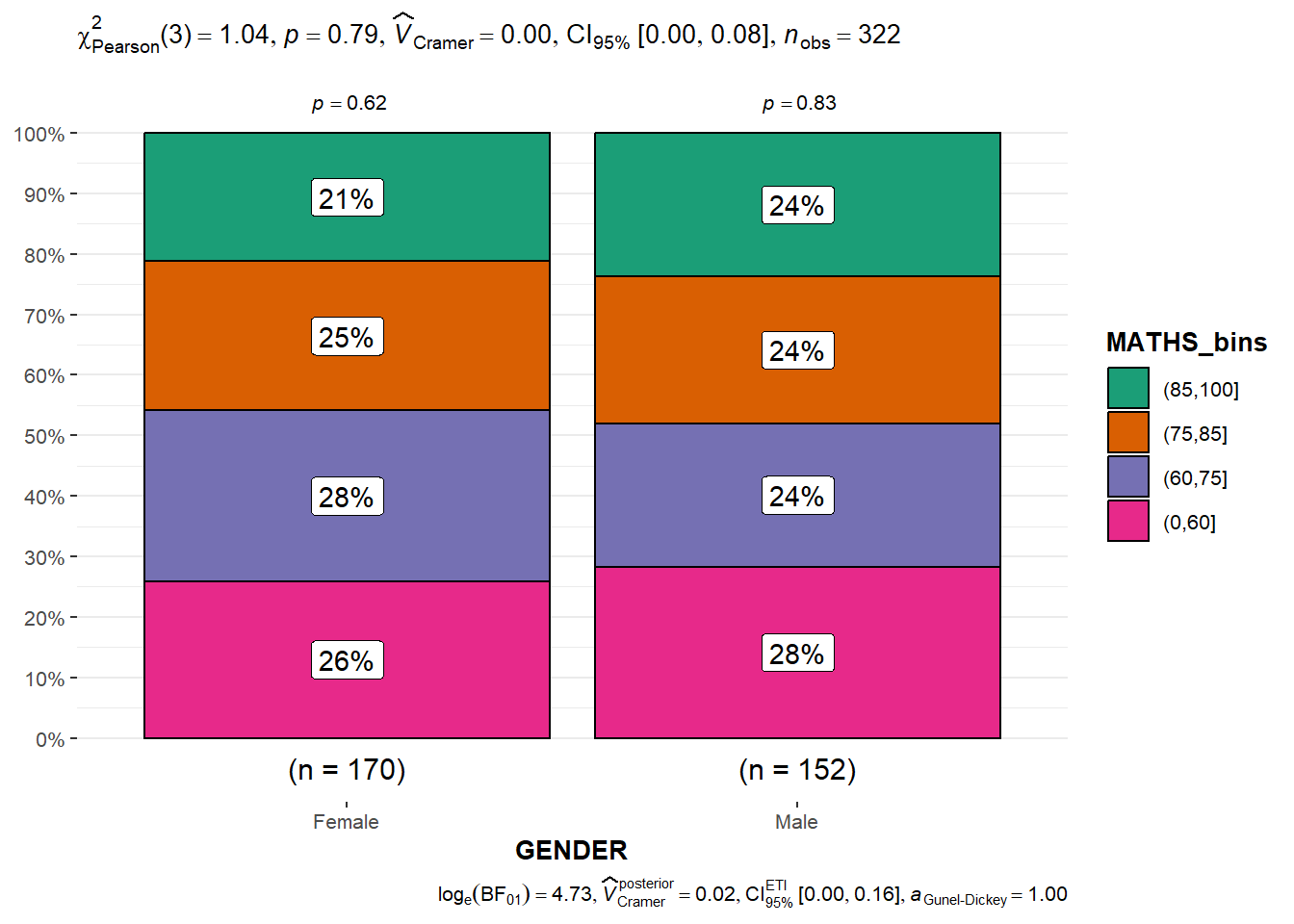

Visualising Uncertainty

Visualizing the uncertainty of point estimates: ggplot2 methods

Preparation

my_sum <- exam %>%
  group_by(RACE) %>%
  summarise(
    n=n(),
    mean=mean(MATHS),
    sd=sd(MATHS)
    ) %>%
  mutate(se=sd/sqrt(n-1))

knitr::kable(head(my_sum), format = 'html')

RACE	n	mean	sd	se
Chinese	193	76.50777	15.69040	1.132357
Indian	12	60.66667	23.35237	7.041005
Malay	108	57.44444	21.13478	2.043177
Others	9	69.66667	10.72381	3.791438

Plotting standard error bars of point estimates

ggplot(my_sum) +
  geom_errorbar(
    aes(x=RACE, 
        ymin=mean-se, 
        ymax=mean+se), 
    width=0.2, 
    colour="black", 
    alpha=0.9, 
    linewidth=0.5) +
  geom_point(aes
           (x=RACE, 
            y=mean), 
           stat="identity", 
           color="red",
           size = 1.5,
           alpha=1) +
  ggtitle("Standard error of mean maths score by rac")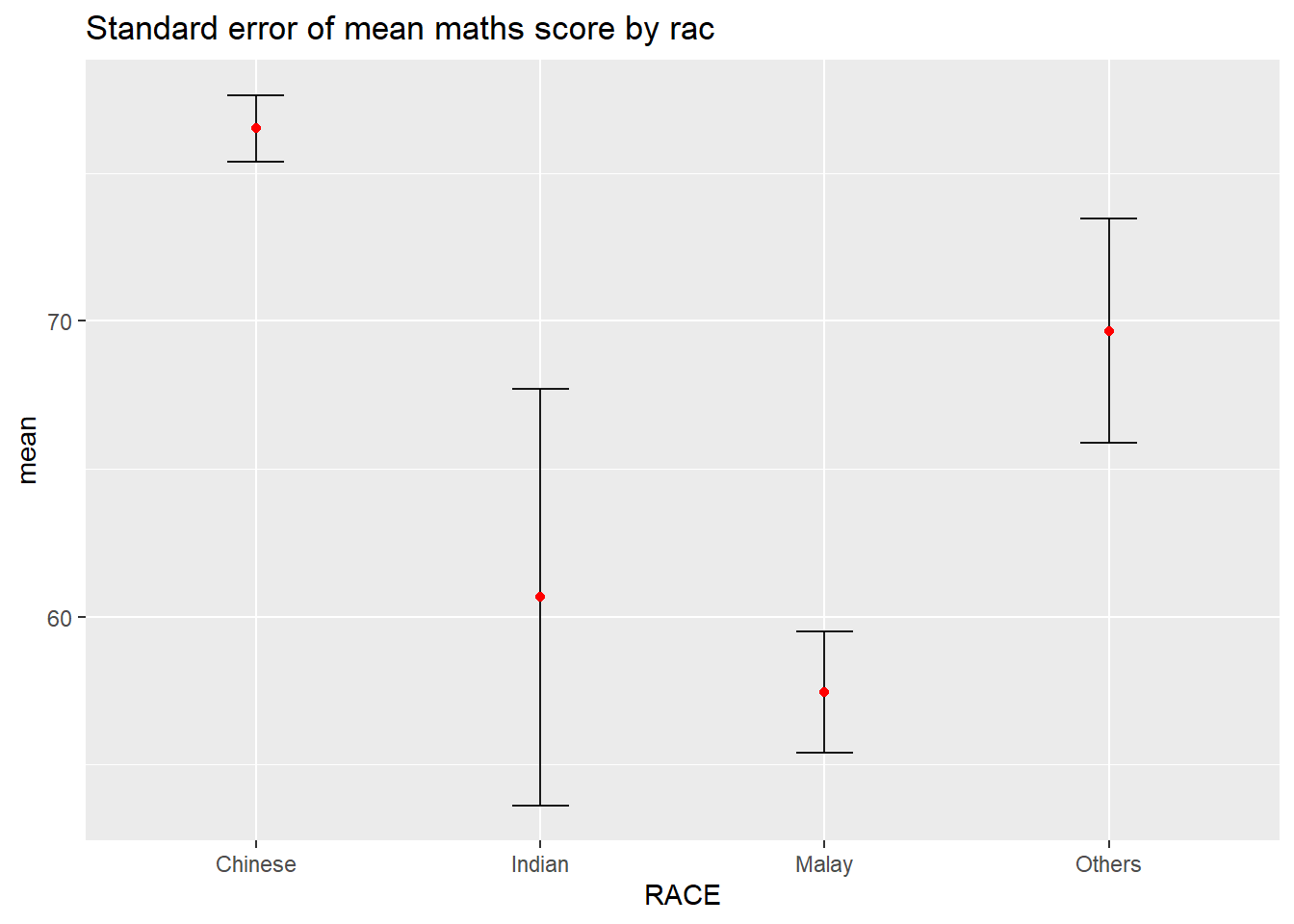

Plotting confidence interval of point estimates

ggplot(my_sum) +
  geom_errorbar(
    aes(x=reorder(RACE, -mean), 
        ymin=mean-1.96*se, 
        ymax=mean+1.96*se), 
    width=0.2, 
    colour="black", 
    alpha=0.9, 
    linewidth=0.5) +
  geom_point(aes
           (x=RACE, 
            y=mean), 
           stat="identity", 
           color="red",
           size = 1.5,
           alpha=1) +
  labs(x = "Maths score",
       title = "95% confidence interval of mean maths score by race")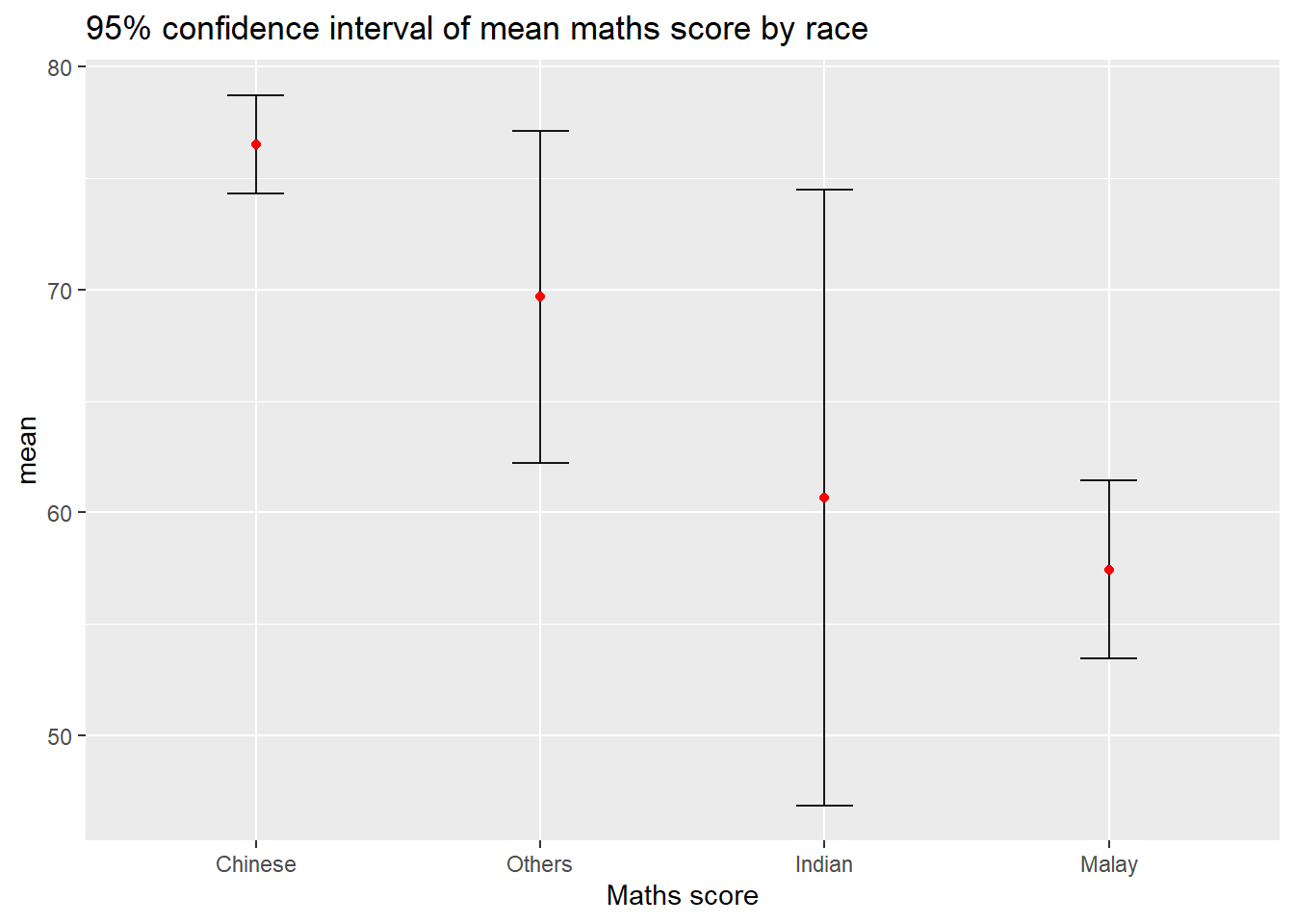

Visualizing the uncertainty of point estimates with interactive error bars

shared_df = SharedData$new(my_sum)

bscols(widths = c(5,7),
       ggplotly(
         ggplot(shared_df) +
           geom_errorbar(aes(
             x = reorder(RACE, -mean),
             ymin = mean - 2.58 * se,
             ymax = mean + 2.58 * se),
             linewidth = 0.5, colour = "black", alpha = 0.9) +
           geom_point(aes(
             x = RACE,
             y = mean,
             text = paste("Race:", RACE,
                          "<br>N:", n,
                          "<br>Avg. Scores:", round(mean, 2),
                          "<br>99% CI:[", round((mean - 2.58 * se), 2), ",",
                          round((mean + 2.58 * se), 2), "]")),
             stat = "identity",
             color = "red", size = 1.5, alpha = 1) +
           xlab("Race") +
           ylab("Average Scores") +
           theme_minimal() +
           theme(axis.text.x = element_text(angle = 45, vjust = 0.5, hjust = 1)) +
           ggtitle("99% Confidence interval of average\nmaths scores by race"),
         tooltip = "text"
       ),
       DT::datatable(shared_df,
                     rownames = FALSE,
                     class = "compact",
                     width = "100%",
                     extensions = 'Buttons',
                     options = list(
                       dom = 'Blfrtip',
                       pageLength = 10,
                       scrollX = TRUE
                     ),
                     colnames = c("No. of pupils", "Avg Scores", "Std Dev", "Std Error")) %>%
         formatRound(columns = c('mean', 'sd', 'se'), digits = 2)
)

Visualising Uncertainty: ggdist package

Visualizing the uncertainty of point estimates: ggdist methods

exam %>%
  ggplot(aes(x = RACE, 
             y = MATHS)) +
  stat_pointinterval() +
  labs(
    title = "Visualising confidence intervals of mean math score",
    subtitle = "Mean Point + Multiple-interval plot")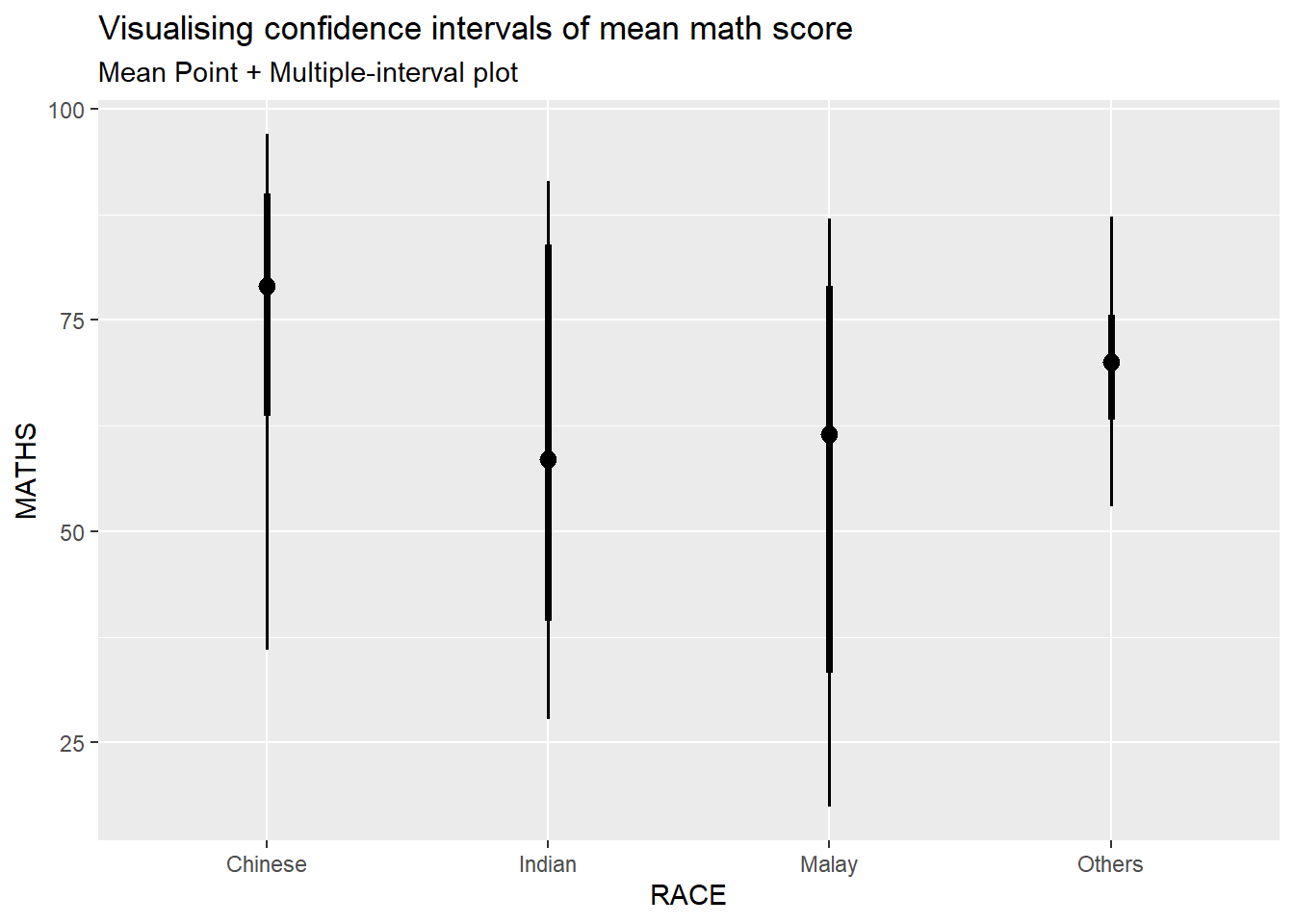

exam %>%
  ggplot(aes(x = RACE, y = MATHS)) +
  stat_pointinterval(.width = 0.95,
  .point = median,
  .interval = qi) +
  labs(
    title = "Visualising confidence intervals of median math score",
    subtitle = "Median Point + Multiple-interval plot")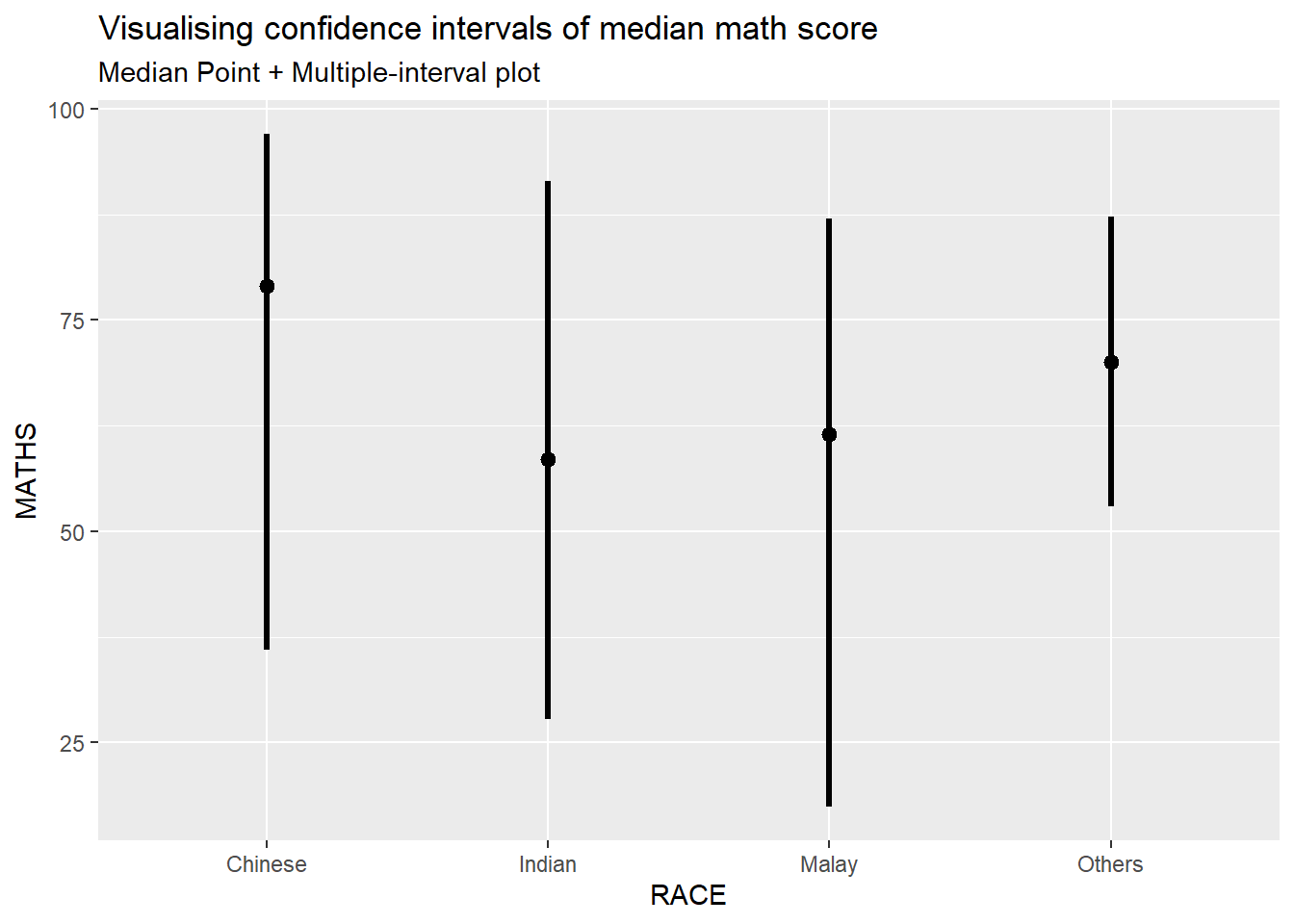

Visualizing the uncertainty of point estimates: ggdist methods

exam %>%
  ggplot(aes(x = RACE, 
             y = MATHS)) +
  stat_pointinterval(
    show.legend = FALSE) +   
  labs(
    title = "Visualising confidence intervals of mean math score",
    subtitle = "Mean Point + Multiple-interval plot")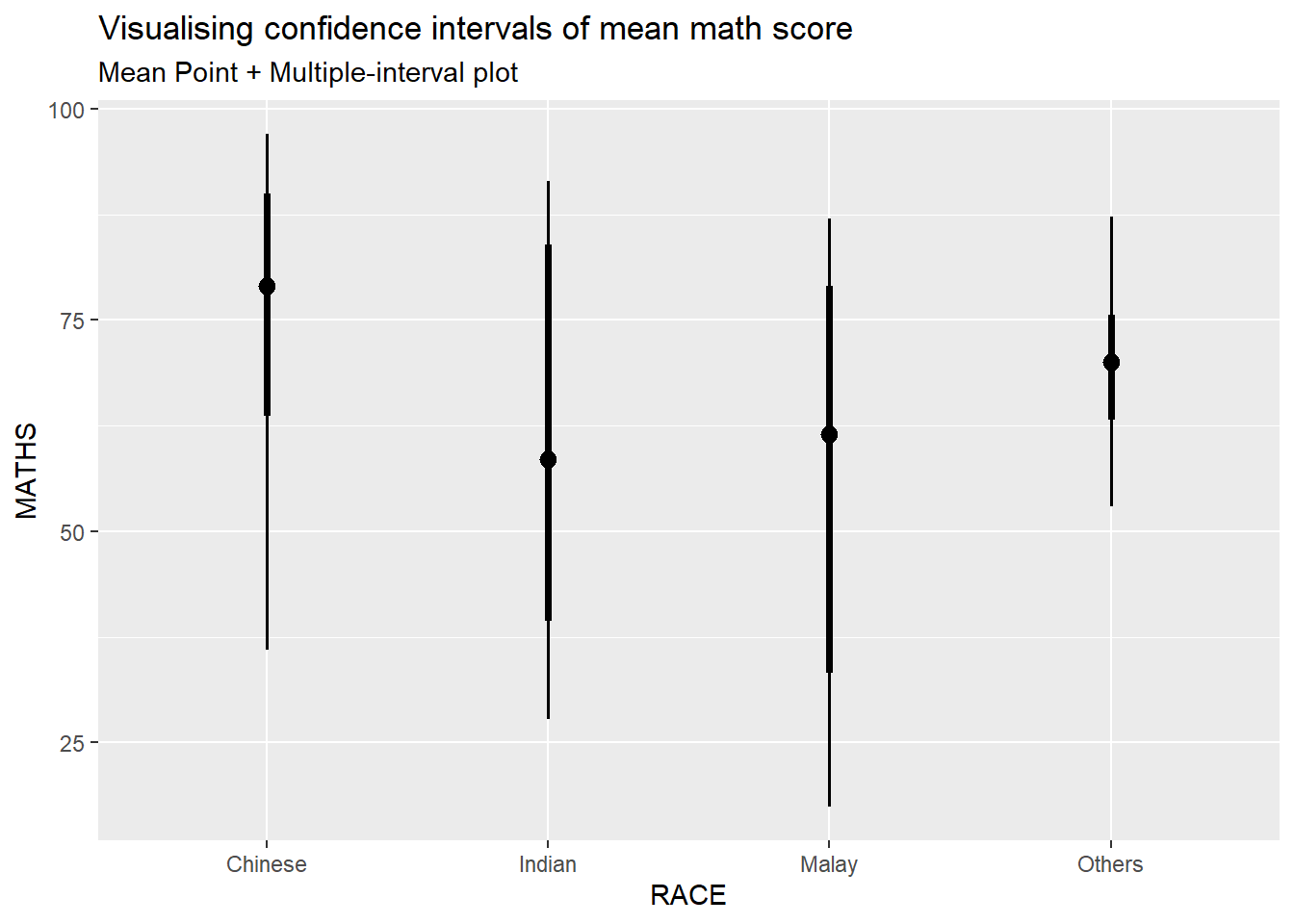

Visualizing the uncertainty of point estimates: ggdist methods

exam %>%
  ggplot(aes(x = RACE, 
             y = MATHS)) +
  stat_gradientinterval(   
    fill = "skyblue",      
    show.legend = TRUE     
  ) +                        
  labs(
    title = "Visualising confidence intervals of mean math score",
    subtitle = "Gradient + interval plot")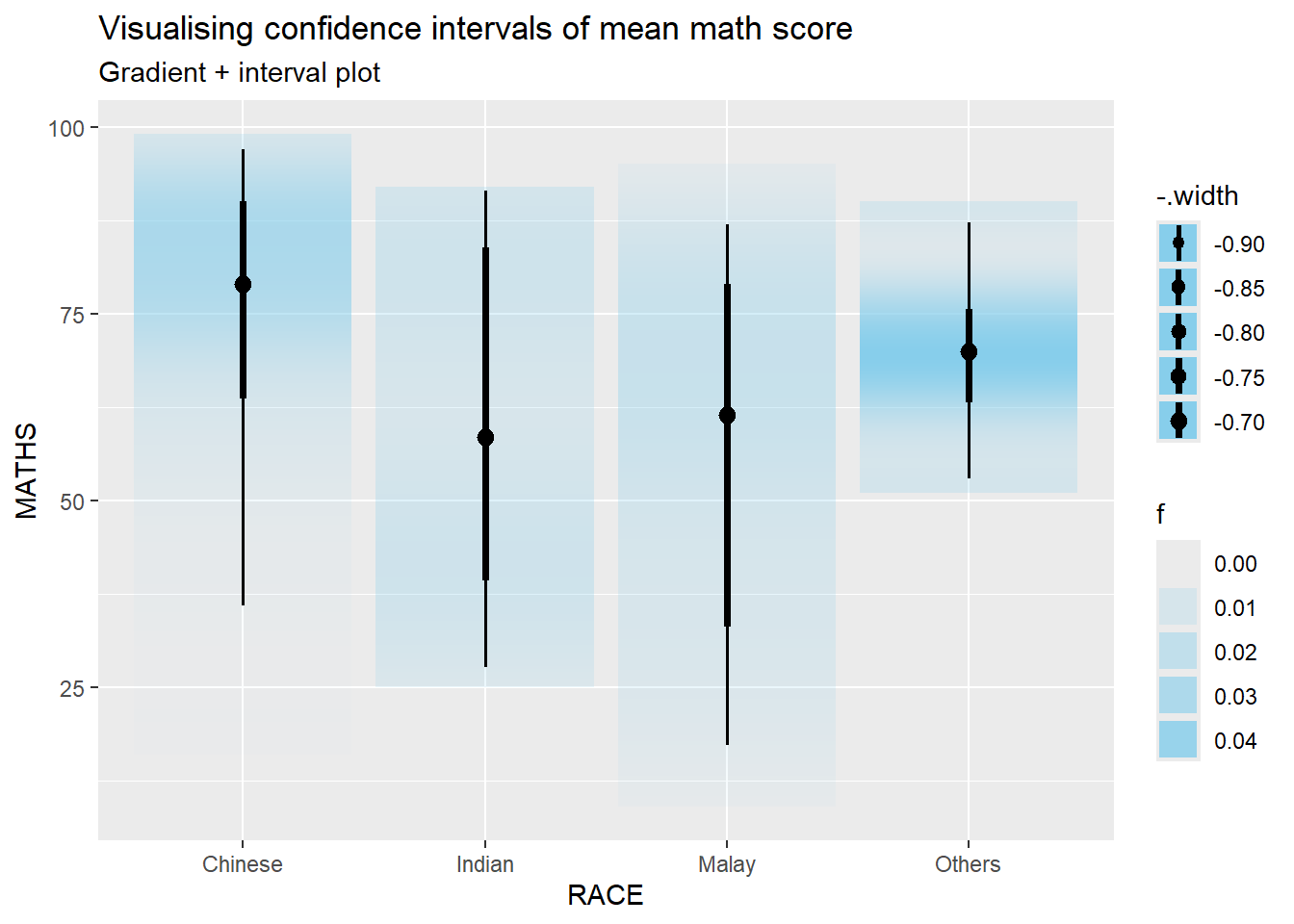

Visualising Uncertainty with Hypothetical Outcome Plots (HOPs)

Installing ungeviz package

devtools::install_github("wilkelab/ungeviz")

library(ungeviz)

ggplot(data = exam, 
       (aes(x = factor(RACE), 
            y = MATHS))) +
  geom_point(position = position_jitter(
    height = 0.3, 
    width = 0.05), 
    size = 0.4, 
    color = "#0072B2", 
    alpha = 1/2) +
  geom_hpline(data = sampler(25, 
                             group = RACE), 
              height = 0.6, 
              color = "#D55E00") +
  theme_bw() + 
  transition_states(.draw, 1, 3)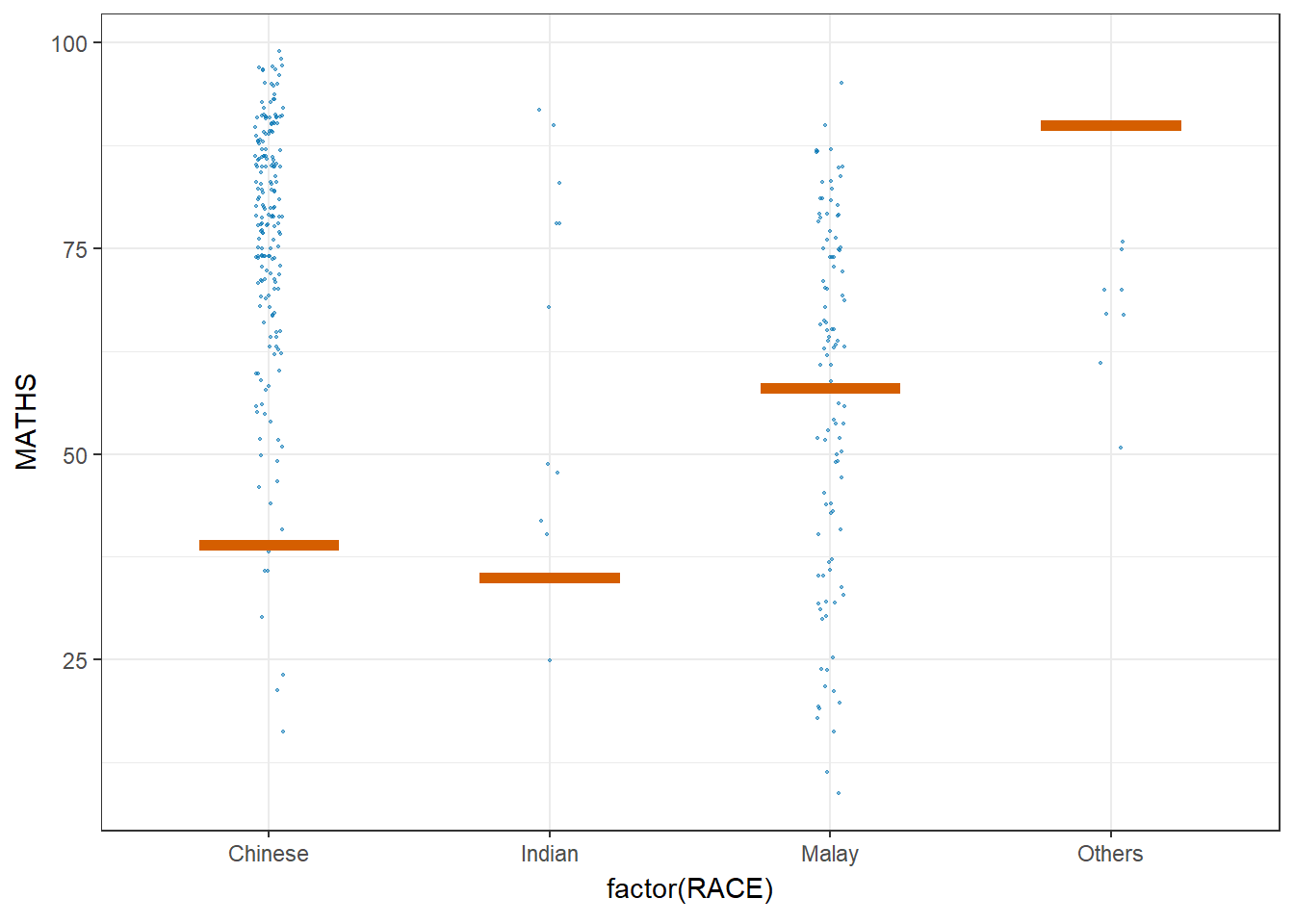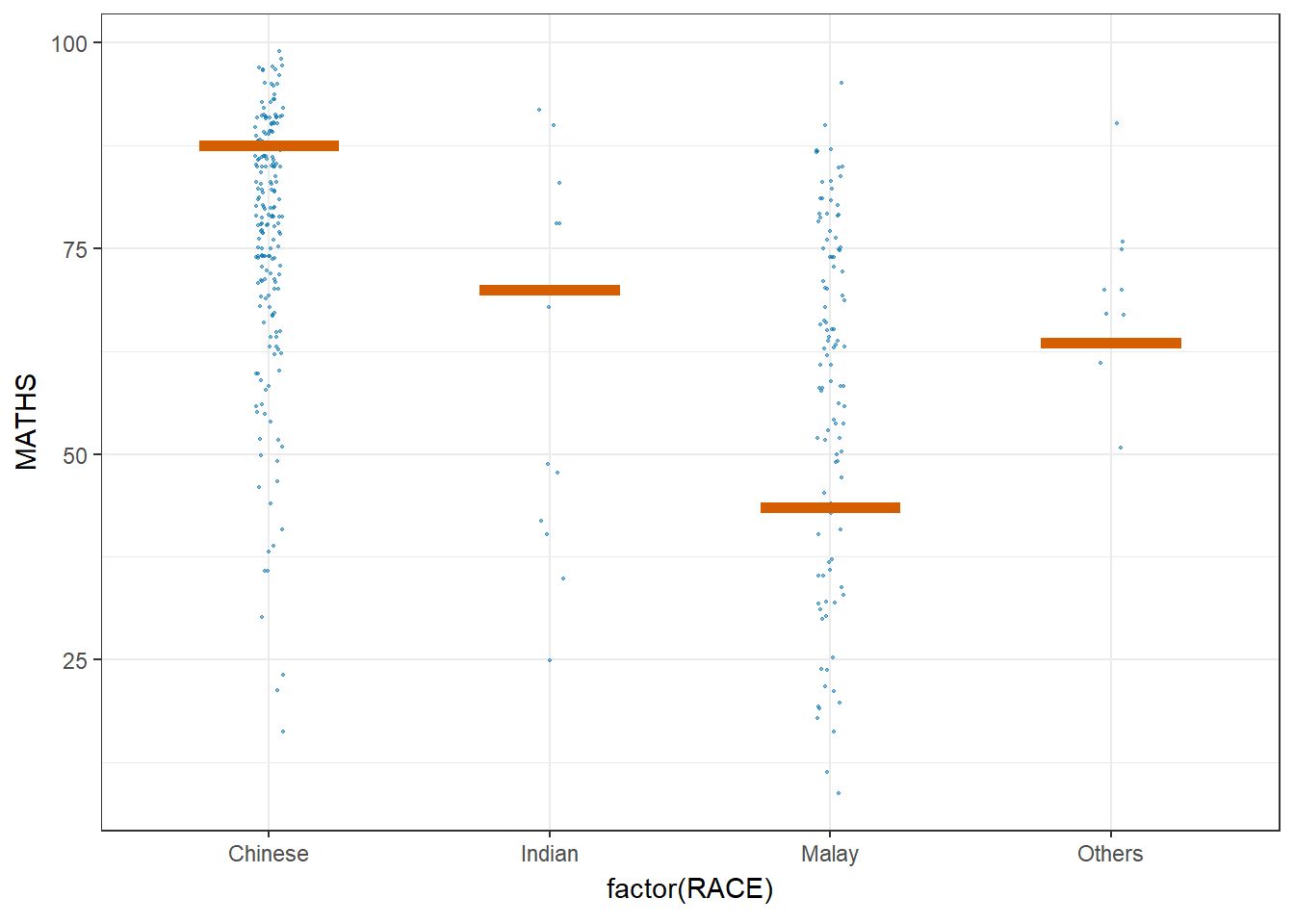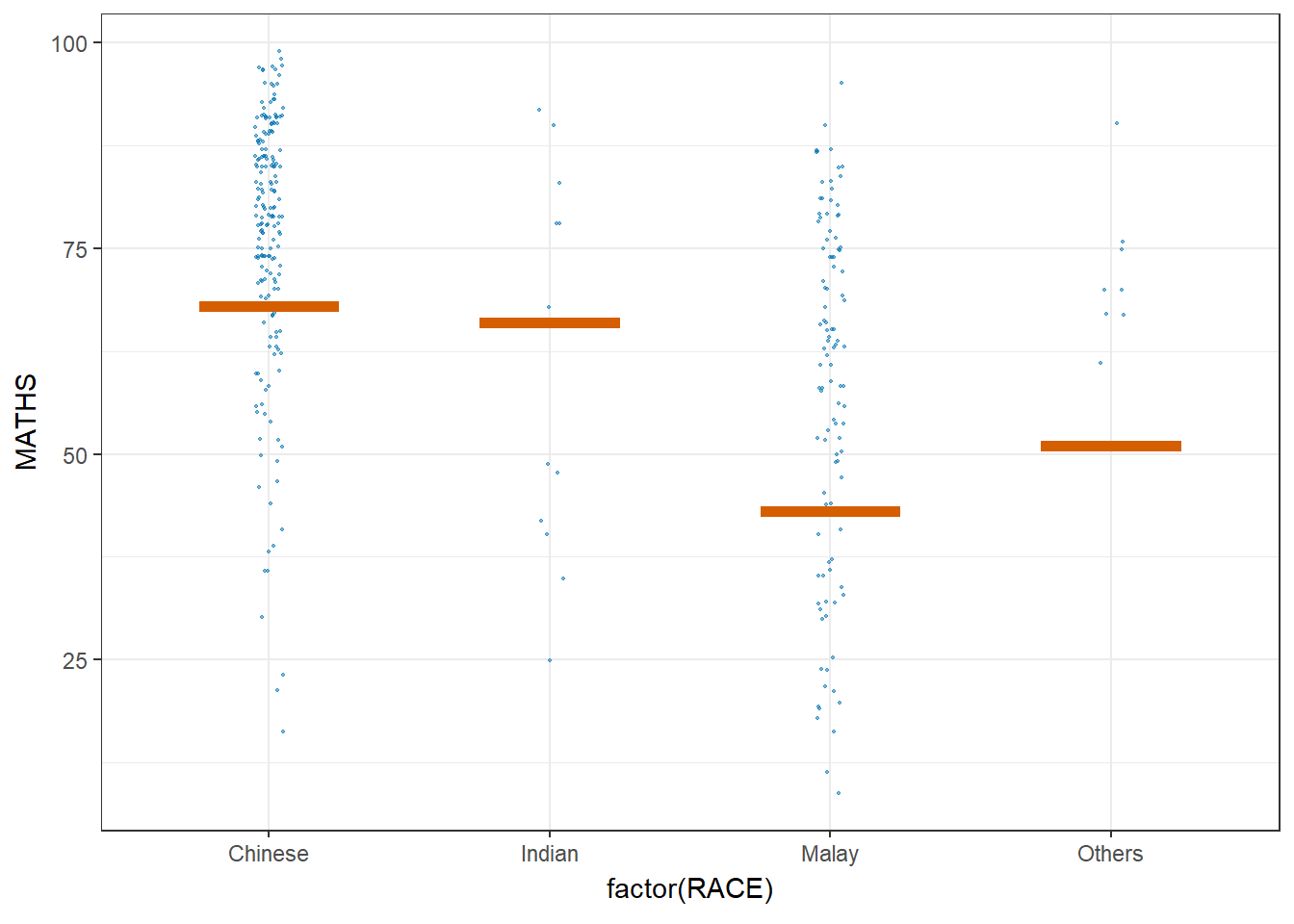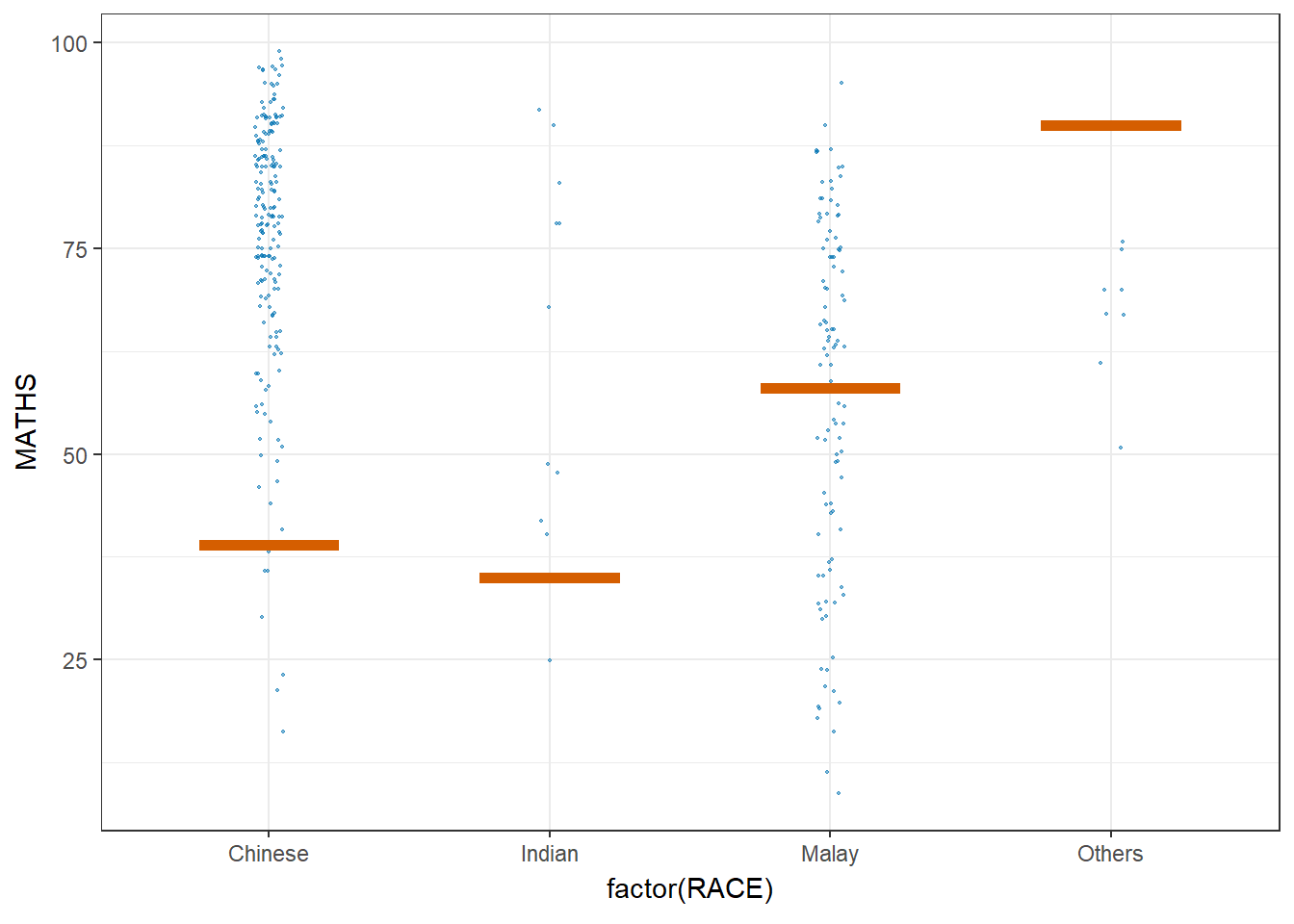

Funnel Plots for Fair Comparisons

FunnelPlotR methods

FunnelPlotR methods: The basic plot

funnel_plot(
  .data = covid19,
  numerator = Positive,
  denominator = Death,
  group = `Sub-district`
)

A funnel plot object with 267 points of which 0 are outliers. 
Plot is adjusted for overdispersion.

FunnelPlotR methods: Makeover 1

funnel_plot(
  .data = covid19,
  numerator = Death,
  denominator = Positive,
  group = `Sub-district`,
  data_type = "PR",     #<<
  xrange = c(0, 6500),  #<<
  yrange = c(0, 0.05)   #<<
)

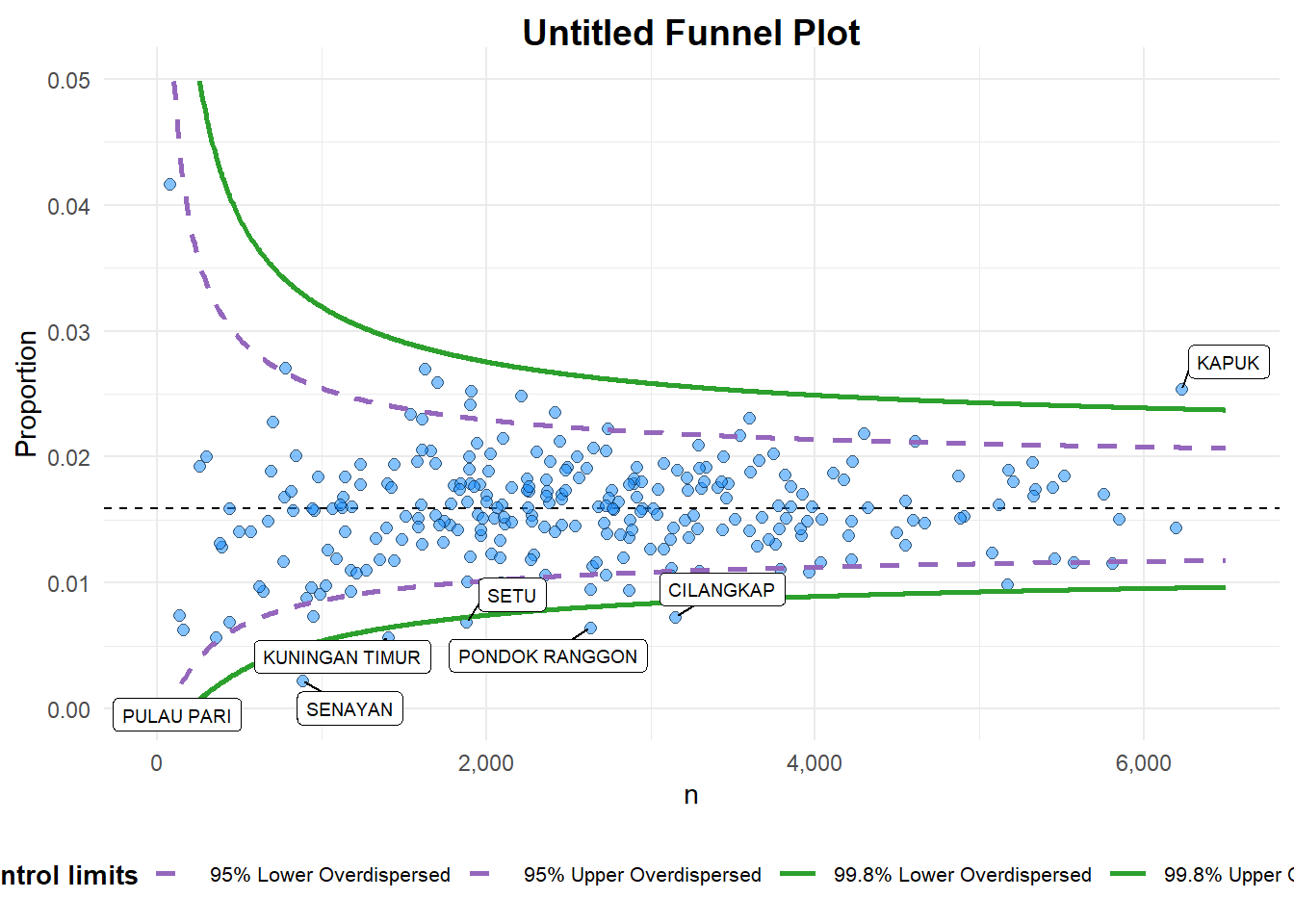
A funnel plot object with 267 points of which 7 are outliers. 
Plot is adjusted for overdispersion.

FunnelPlotR methods: Makeover 2

funnel_plot(
  .data = covid19,
  numerator = Death,
  denominator = Positive,
  group = `Sub-district`,
  data_type = "PR",   
  xrange = c(0, 6500),  
  yrange = c(0, 0.05),
  label = NA,
  title = "Cumulative COVID-19 Fatality Rate by Cumulative Total Number of COVID-19 Positive Cases", #<<           
  x_label = "Cumulative COVID-19 Positive Cases", #<<
  y_label = "Cumulative Fatality Rate"  #<<
)

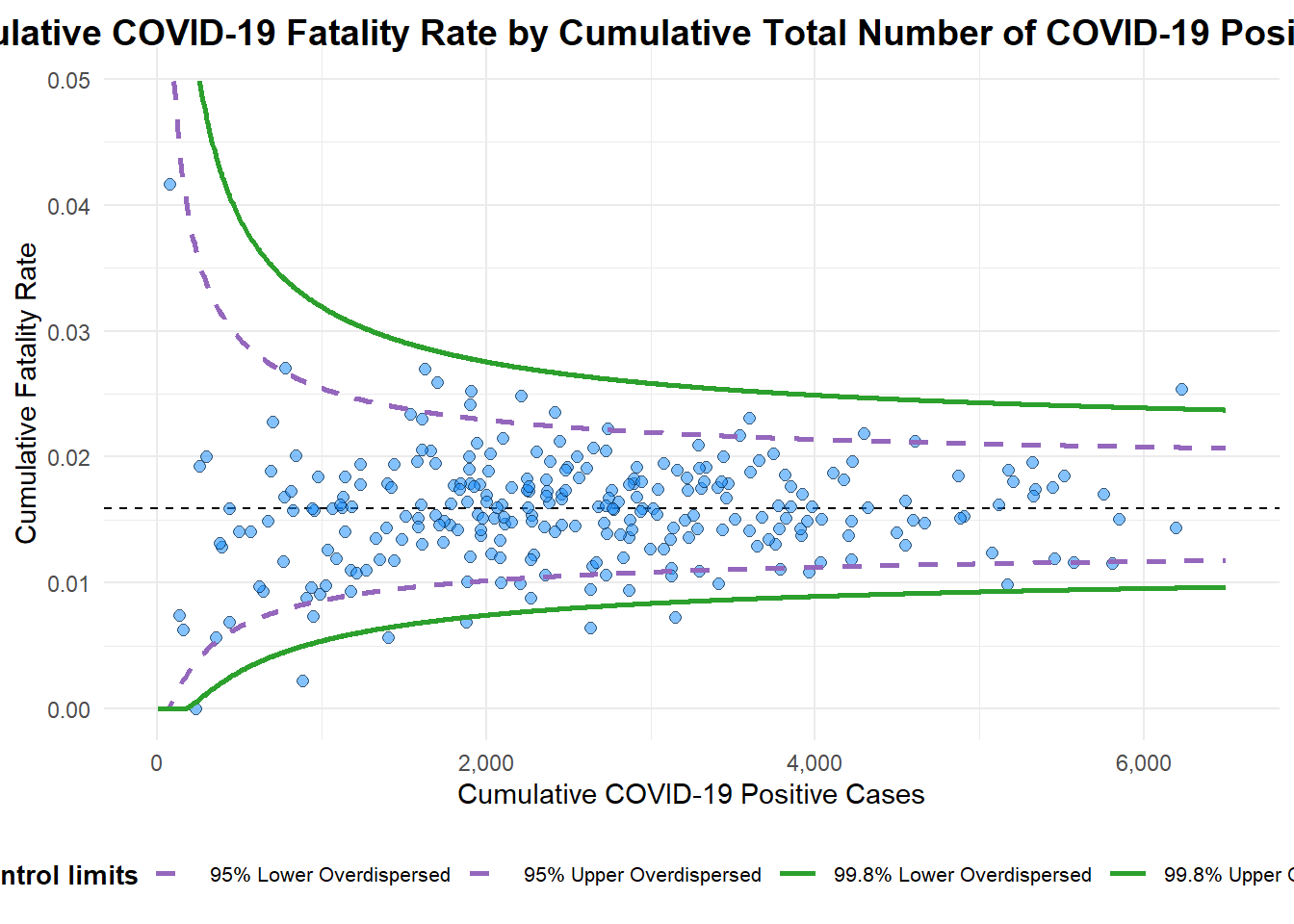
A funnel plot object with 267 points of which 7 are outliers. 
Plot is adjusted for overdispersion.

Funnel Plot for Fair Visual Comparison: ggplot2 methods

Computing the basic derived fields

df <- covid19 %>%
  mutate(rate = Death / Positive) %>%
  mutate(rate.se = sqrt((rate*(1-rate)) / (Positive))) %>%
  filter(rate > 0)

fit.mean <- weighted.mean(df$rate, 1/df$rate.se^2)

Calculate lower and upper limits for 95% and 99.9% CI

number.seq <- seq(1, max(df$Positive), 1)
number.ll95 <- fit.mean - 1.96 * sqrt((fit.mean*(1-fit.mean)) / (number.seq)) 
number.ul95 <- fit.mean + 1.96 * sqrt((fit.mean*(1-fit.mean)) / (number.seq)) 
number.ll999 <- fit.mean - 3.29 * sqrt((fit.mean*(1-fit.mean)) / (number.seq)) 
number.ul999 <- fit.mean + 3.29 * sqrt((fit.mean*(1-fit.mean)) / (number.seq)) 
dfCI <- data.frame(number.ll95, number.ul95, number.ll999, 
                   number.ul999, number.seq, fit.mean)

Plotting a static funnel plot

p <- ggplot(df, aes(x = Positive, y = rate)) +
  geom_point(aes(label=`Sub-district`), 
             alpha=0.4) +
  geom_line(data = dfCI, 
            aes(x = number.seq, 
                y = number.ll95), 
            size = 0.4, 
            colour = "grey40", 
            linetype = "dashed") +
  geom_line(data = dfCI, 
            aes(x = number.seq, 
                y = number.ul95), 
            size = 0.4, 
            colour = "grey40", 
            linetype = "dashed") +
  geom_line(data = dfCI, 
            aes(x = number.seq, 
                y = number.ll999), 
            size = 0.4, 
            colour = "grey40") +
  geom_line(data = dfCI, 
            aes(x = number.seq, 
                y = number.ul999), 
            size = 0.4, 
            colour = "grey40") +
  geom_hline(data = dfCI, 
             aes(yintercept = fit.mean), 
             size = 0.4, 
             colour = "grey40") +
  coord_cartesian(ylim=c(0,0.05)) +
  annotate("text", x = 1, y = -0.13, label = "95%", size = 3, colour = "grey40") + 
  annotate("text", x = 4.5, y = -0.18, label = "99%", size = 3, colour = "grey40") + 
  ggtitle("Cumulative Fatality Rate by Cumulative Number of COVID-19 Cases") +
  xlab("Cumulative Number of COVID-19 Cases") + 
  ylab("Cumulative Fatality Rate") +
  theme_light() +
  theme(plot.title = element_text(size=12),
        legend.position = c(0.91,0.85), 
        legend.title = element_text(size=7),
        legend.text = element_text(size=7),
        legend.background = element_rect(colour = "grey60", linetype = "dotted"),
        legend.key.height = unit(0.3, "cm"))
p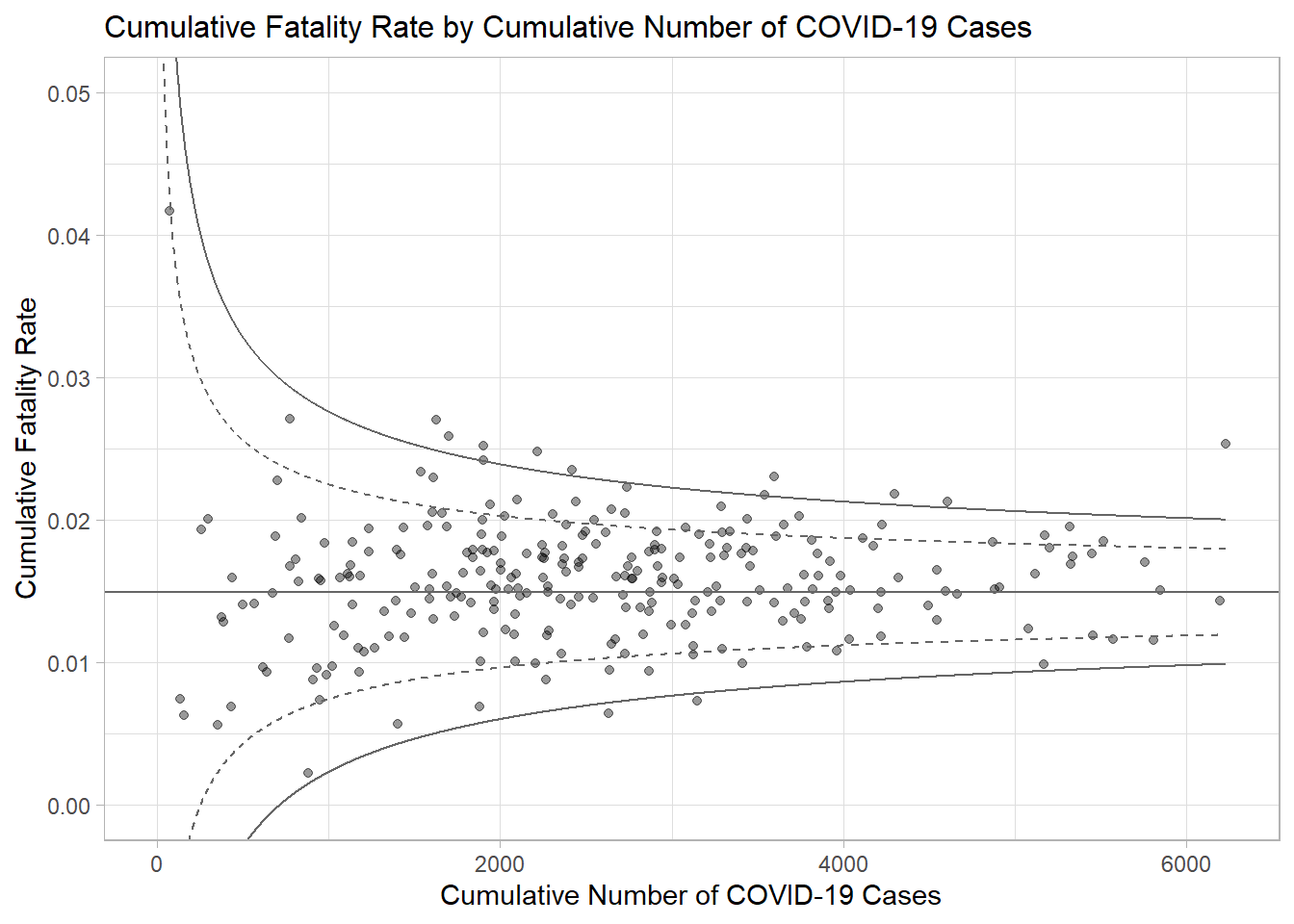

Interactive Funnel Plot: plotly + ggplot2

fp_ggplotly <- ggplotly(p,
  tooltip = c("label", 
              "x", 
              "y"))
fp_ggplotly